Probleemstelling:
Targeted drug design: thermodynamic and kinetic selectivity
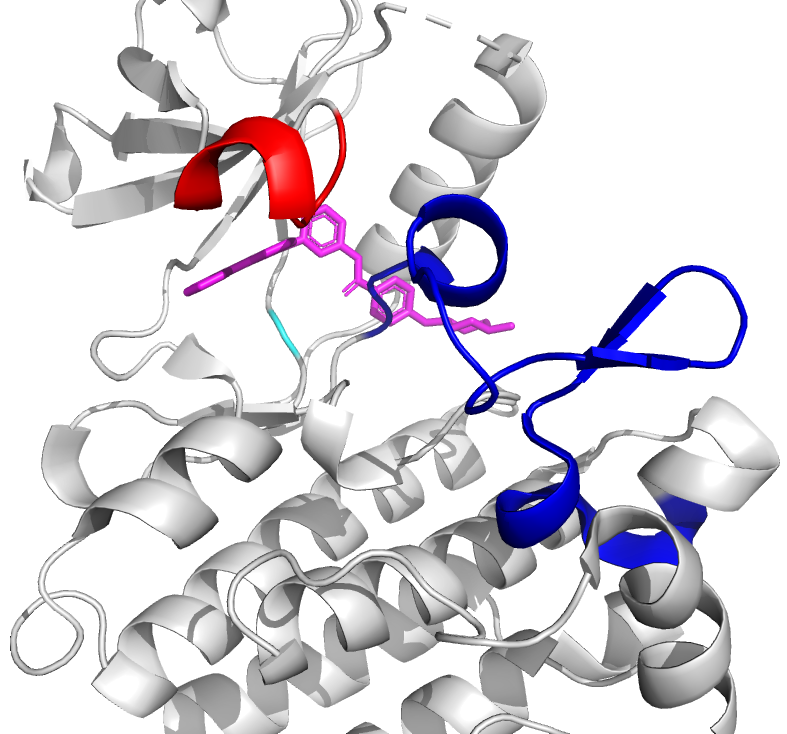
The human proteome consists of a tightly regulated network of proteins, where specific sites on these proteins allow them to interact with other proteins, small (drug) molecules, antigens, or ligands in general. The result of such binding interaction is a conformational change of the target protein, where it takes on a – sometimes slightly – different 3D structural position, which allows the target protein to project new binding sites, or to transfer functional groups from one protein to another. In other words, the binding interaction activates or inhibits a specific function of the target protein, which enables the interaction with yet another protein or ligand, and thus forms one branch of a signaling cascade in the protein network.
As the name reveals, targeted drug design deals with the development of ligands that bind to a target protein, to inhibit or activate functionality depending on the toxic nature of the protein. Generally, the structure of the target protein and its binding sites are known a priori, and one searches for compatible ligands. In the last decades, the quest thereof has been dominated by structural and thermodynamical considerations, where candidate ligands are ranked by their equilibrium constants Kd. This constant, also known as the dissociation constant, describes the fraction of target-proteins that would be bound to the ligand at equilibrium conditions, and in particular, at constant ligand concentration. A schematic picture of protein-ligand binding is given in Figure 1, where it is seen that the equilibrium constant is given by the ratio of the kinetic rate constants koff and kon. From physical chemistry, it is known that Kd is proportional to the Boltzmann constant associated with the free energy difference of the bound and unbound states (Figure 1, left).
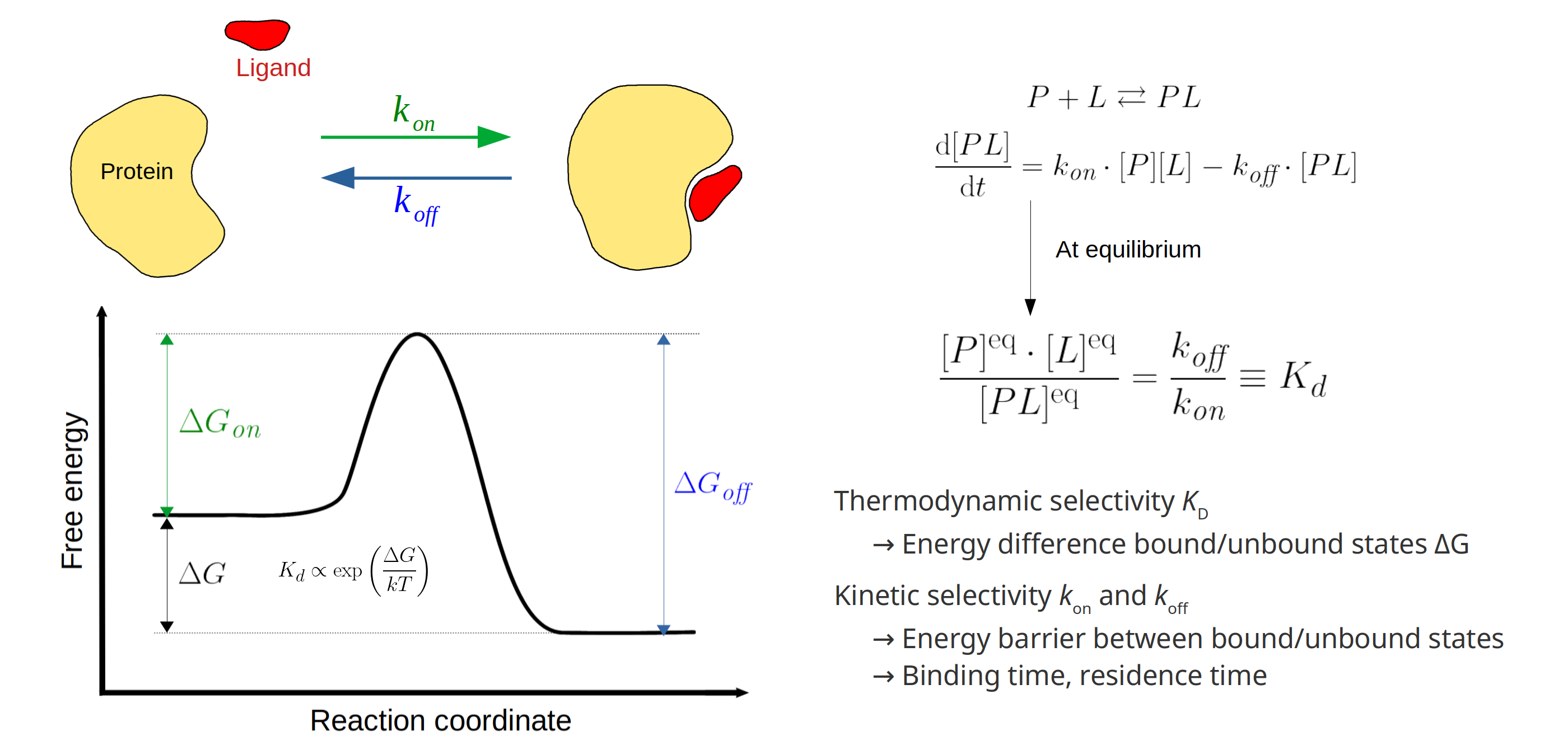
Figure 1: Left: schematic picture of the Protein-Ligand (P-L) binding free energy profile. The equilibrium constant Kd is fully described by the free energy difference deltaG of the unbound and bound states, describing the strength of the P-L bound complex. For this reason, Kd has served as the dominant parameter in targeted drug design. However, the binding reaction is almost always accompanied by an energy barrier which is often not negligible, and can highly impact the effectiveness of the candidate ligand in vivo (see text). Right: differential equation accompanying the bimolecular binding reaction, where [P] and [L] denote protein and ligand concentrations, respectively.
While it is true that Kd is a good indicator of binding strength, it has major shortcomings that prove to be detrimental: more than 90% of promising drug molecules fail human trials by off-target toxicity and/or bad overall target selectivity. Indeed, thermodynamic selection based on Kd neglects the existence of a free energy barrier that needs to be overcome during the binding reaction (Figure 1, left). While the final bound state at the target protein may be energetically most favourable, the energy barrier may be sufficiently high that most drug molecules bind to a – potentially toxic – off-target protein with less favourable bound state, but lower energy barrier. To this end, the notion of kinetic selectivity has gained a lot of attention in the latest years, where one tries to obtain the rate constants kon and koff. These parameters hold information about kinetic properties of the protein-ligand interaction, such as the drug residence-time, allowing better profiling of candidate drug molecules and saving costly and time-consuming in vivo experiments.
Molecular dynamics for protein-ligand binding
While experimental techniques provide excellent methods to study proteins, they are time-consuming and expensive. Moreover, probing the proteins’ extremely fast configurational changes and interactions at the atomic scale remains challenging. To this end, computational techniques have been developed for high-throughput applications (e.g. protein-ligand docking in targeted drug design), and molecular dynamics (MD) simulations that provide the fully atomistic picture of proteins. However, binding/residence times are typically multiple milliseconds, seconds, minutes or even hours, while conventional MD simulations are rarely longer than 1 millisecond. The binding interaction is a so-called rare event in simulations, and makes the study of time-dependent parameters (i.e. kinetics) a difficult subject. This thesis will use and develop advanced methodological simulations tools that accelerate the binding process, such that enough binding events are simulated and the significant statistics are achieved at computationally reasonable cost. Principles from statistical physics will be used to retrieve the true dynamics of the binding process as if no acceleration was applied.